动态规划的本质不在于是递推或是递归，也不需要纠结是不是内存换时间。

理解动态规划并不需要数学公式介入，只是完全解释清楚需要点篇幅…首先需要明白哪些问题不是动态规划可以解决的，才能明白为神马需要动态规划。不过好处时顺便也就搞明白了递推贪心搜索和动规之间有什么关系，以及帮助那些总是把动规当成搜索解的同学建立动规的思路。当然熟悉了之后可以直接根据问题的描述得到思路，如果有需要的话再补充吧。

动态规划是对于 某一类问题 的解决方法！！重点在于如何鉴定“某一类问题”是动态规划可解的而不是纠结解决方法是递归还是递推！

怎么鉴定dp可解的一类问题需要从计算机是怎么工作的说起…计算机的本质是一个状态机，内存里存储的所有数据构成了当前的状态，CPU只能利用当前的状态计算出下一个状态（不要纠结硬盘之类的外部存储，就算考虑他们也只是扩大了状态的存储容量而已，并不能改变下一个状态只能从当前状态计算出来这一条铁律）

当你企图使用计算机解决一个问题是，其实就是在思考如何将这个问题表达成状态（用哪些变量存储哪些数据）以及如何在状态中转移（怎样根据一些变量计算出另一些变量）。所以所谓的空间复杂度就是为了支持你的计算所必需存储的状态最多有多少，所谓时间复杂度就是从初始状态到达最终状态中间需要多少步！

太抽象了还是举个例子吧：

比如说我想计算第100个非波那契数，每一个非波那契数就是这个问题的一个状态，每求一个新数字只需要之前的两个状态。所以同一个时刻，最多只需要保存两个状态，空间复杂度就是常数；每计算一个新状态所需要的时间也是常数且状态是线性递增的，所以时间复杂度也是线性的。

上面这种状态计算很直接，只需要依照固定的模式从旧状态计算出新状态就行（a[i]=a[i-1]+a[i-2]），不需要考虑是不是需要更多的状态，也不需要选择哪些旧状态来计算新状态。对于这样的解法，我们叫递推。

非波那契那个例子过于简单，以至于让人忽视了阶段的概念，所谓阶段是指随着问题的解决，在同一个时刻可能会得到的不同状态的集合。非波那契数列中，每一步会计算得到一个新数字，所以每个阶段只有一个状态。想象另外一个问题情景，假如把你放在一个围棋棋盘上的某一点，你每一步只能走一格，因为你可以东南西北随便走，所以你当你同样走四步可能会处于很多个不同的位置。从头开始走了几步就是第几个阶段，走了n步可能处于的位置称为一个状态，走了这n步所有可能到达的位置的集合就是这个阶段下所有可能的状态。

现在问题来了，有了阶段之后，计算新状态可能会遇到各种奇葩的情况，针对不同的情况，就需要不同的算法，下面就分情况来说明一下：

假如问题有n个阶段，每个阶段都有多个状态，不同阶段的状态数不必相同，一个阶段的一个状态可以得到下个阶段的所有状态中的几个。那我们要计算出最终阶段的状态数自然要经历之前每个阶段的某些状态。

好消息是，有时候我们并不需要真的计算所有状态，比如这样一个弱智的棋盘问题：从棋盘的左上角到达右下角最短需要几步。答案很显然，用这样一个弱智的问题是为了帮助我们理解阶段和状态。某个阶段确实可以有多个状态，正如这个问题中走n步可以走到很多位置一样。但是同样n步中，有哪些位置可以让我们在第n+1步中走的最远呢？没错，正是第n步中走的最远的位置。换成一句熟悉话叫做“下一步最优是从当前最优得到的”。所以为了计算最终的最优值，只需要存储每一步的最优值即可，解决符合这种性质的问题的算法就叫贪心。如果只看最优状态之间的计算过程是不是和非波那契数列的计算很像？所以计算的方法是递推。

既然问题都是可以划分成阶段和状态的。这样一来我们一下子解决了一大类问题：一个阶段的最优可以由前一个阶段的最优得到。

如果一个阶段的最优无法用前一个阶段的最优得到呢？

什么你说只需要之前两个阶段就可以得到当前最优？那跟只用之前一个阶段并没有本质区别。最麻烦的情况在于你需要之前所有的情况才行。

再来一个迷宫的例子。在计算从起点到终点的最短路线时，你不能只保存当前阶段的状态，因为题目要求你最短，所以你必须知道之前走过的所有位置。因为即便你当前再的位置不变，之前的路线不同会影响你的之后走的路线。这时你需要保存的是之前每个阶段所经历的那个状态，根据这些信息才能计算出下一个状态！

每个阶段的状态或许不多，但是每个状态都可以转移到下一阶段的多个状态，所以解的复杂度就是指数的，因此时间复杂度也是指数的。哦哦，刚刚提到的之前的路线会影响到下一步的选择，这个令人不开心的情况就叫做有后效性。

刚刚的情况实在太普遍，解决方法实在太暴力，有没有哪些情况可以避免如此的暴力呢？

契机就在于后效性。

有一类问题，看似需要之前所有的状态，其实不用。不妨也是拿最长上升子序列的例子来说明为什么他不必需要暴力搜索，进而引出动态规划的思路。

假装我们年幼无知想用搜索去寻找最长上升子序列。怎么搜索呢？需要从头到尾依次枚举是否选择当前的数字，每选定一个数字就要去看看是不是满足“上升”的性质，这里第i个阶段就是去思考是否要选择第i个数，第i个阶段有两个状态，分别是选和不选。哈哈，依稀出现了刚刚迷宫找路的影子！咦慢着，每次当我决定要选择当前数字的时候，只需要和之前选定的一个数字比较就行了！这是和之前迷宫问题的本质不同！这就可以纵容我们不需要记录之前所有的状态啊！既然我们的选择已经不受之前状态的组合的影响了，那时间复杂度自然也不是指数的了啊！虽然我们不在乎某序列之前都是什么元素，但我们还是需要这个序列的长度的。所以我们只需要记录以某个元素结尾的LIS长度就好！因此第i个阶段的最优解只是由前i-1个阶段的最优解得到的，然后就得到了DP方程（感谢

指正）

所以一个问题是该用递推、贪心、搜索还是动态规划，完全是由这个问题本身阶段间状态的转移方式决定的！

每个阶段只有一个状态->递推；

每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心；

每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索；

每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。

每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到

这个性质叫做最优子结构；

而不管之前这个状态是如何得到的

这个性质叫做无后效性。

另：其实动态规划中的最优状态的说法容易产生误导，以为只需要计算最优状态就好，LIS问题确实如此，转移时只用到了每个阶段“选”的状态。但实际上有的问题往往需要对每个阶段的所有状态都算出一个最优值，然后根据这些最优值再来找最优状态。比如背包问题就需要对前i个包（阶段）容量为j时（状态）计算出最大价值。然后在最后一个阶段中的所有状态种找到最优值。

维基百科上对于动态规划是这么定义的：

dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

Ref: Dynamic programming

也就是说，动态规划一定是具备了以下三个特点：

1. 把原来的问题分解成了几个相似的子问题。（强调“相似子问题”）
2. 所有的子问题都只需要解决一次。（强调“只解决一次”）
3. 储存子问题的解。（强调“储存”）

直接读这个定义还是比较玄乎抽象的。这里，我想结合两个实际例子，来分别回答题主提出的两个问题：

1. 什么是动态规划？
2. 动态规划的意义是什么？

我们来看看最经典的——斐波那契数列(Fibonacci)的例子！

1， 1， 2， 3， 5， 8， 13 ，21 ...

如果我们把第n个斐波拉契数记作 Fibonacci(n)，那么怎样利用动态规划来计算这个数呢？

根据动态规划的三个特点，首先，我们需要把原问题分解成几个相似的子问题。这里还蛮清晰的啦，子问题就是这两个：Fibonacci(n-1) 和 Fibonacci(n-2)。

而原问题和子问题之间的关系是：

(其中Fibonacci(0)=Fibonacci(1)=1)

假设我们现在需要计算n=6的时候，斐波拉契的值，那么我们就需要计算他的子问题Fibonacci(5)和Fibonacci(4)。同理对于Fibonacci(5)我们需要计算Fibonacci(4)和Fibonacci(3)，对于Fibonacci(4)我们需要计算Fibonacci(3)和Fibonacci(2)。这样的话，最后我们需要计算的东西如下图——由最顶向下不停的分解问题，最后往上返回结果。

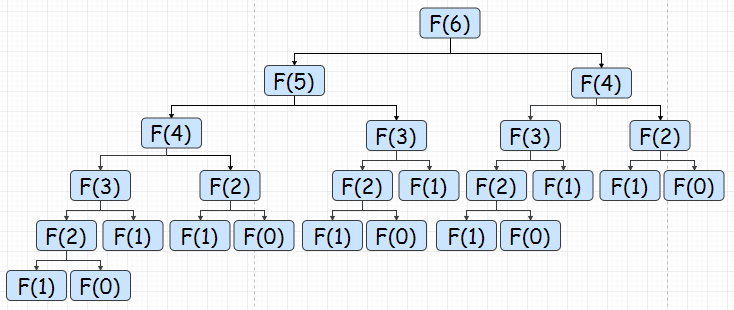
显然，这是一个非常低效的方法，因为其中有大量的重复计算。并且不满足动态规划的第二个特点：“所有的子问题都只需要解决一次“。

这个问题很好解决，我们只需要利用动态规划的第三个特点——”储存子问题的解“就可以了。比如，如果已经计算过Fibonacci(3)，那么把结果储存起来，其他地方碰到需要求Fibonacci(3)的时候，就不需要计算，直接调用结果就行。这样做之后，蓝色表示需要进行计算的，白色表示可以直接从存储中取得结果的：

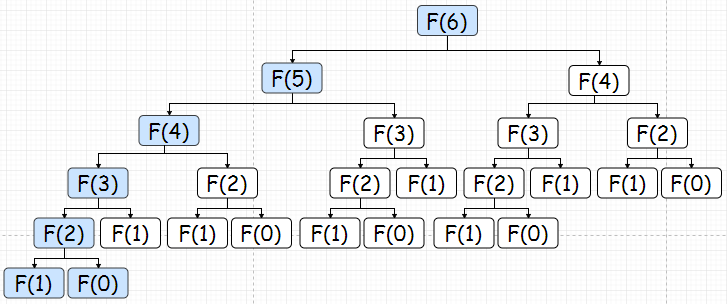
也就是如下的计算（红色箭头表示调用了储存的数据，并未进行计算）：

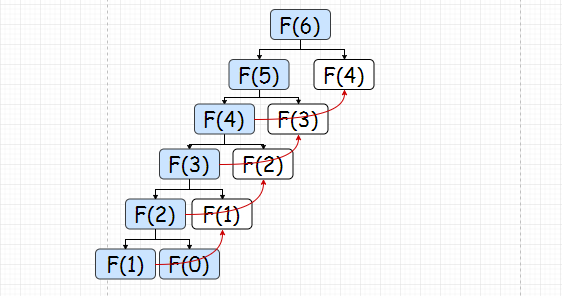
看到这里，你可能会问这样一个问题，如果要计算Fibonacci(6)的话，何必这样大费周章的又是分解问题，又是储存的呢？直接这样从Fibonacci(0)和Fibonacci(1)开始一直往上一步步加就是了啊，看：

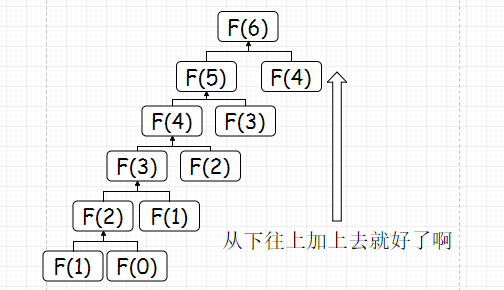
又直观又简洁，为啥要用动态规划呢？又要分解问题又要储存啥的。似乎看起来，动态规划的作用并不大的样子。

对于上面斐波拉契数列的例子，其实还真就是这样。动态规划至顶向下的算法和暴力的从底向上的算法其实没有太大区别。

我们再来看另外一个列子：求一个数列中最长上升子数列的长度（LIS）的问题。

比如，给一个数列：

他的最长上升子数列就是：

[1,2,3,4], 长度为4，所以这个数列的最长上升子数列长度就是4。

对于这类问题我们如何求解呢？我们这次先用暴力来解一下试试，还是用上面那个数列作为例子：

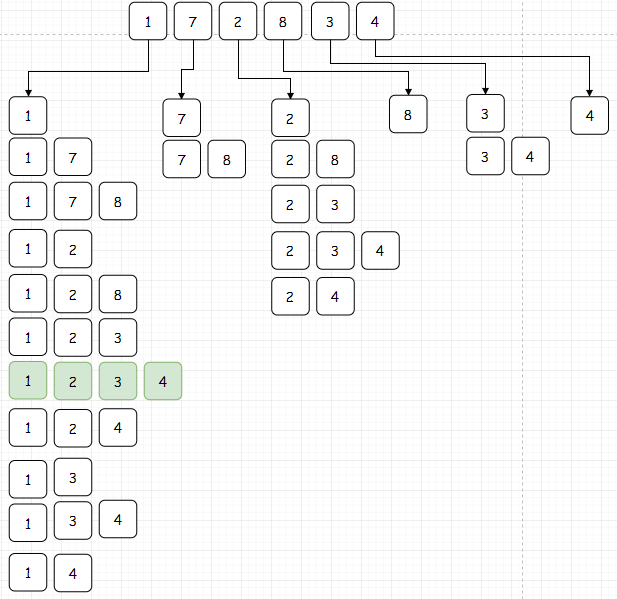
古老的穷举法！直接这样找出所有的上升子序列，然后用肉眼观察哪个是最长的。显然，1,2,3,4是最长的，所以最长上升子序列的长度是4。

很明显，这样进行穷举的话时间复杂度就是 .

这就太消耗时间了。我们现在用动态规划试一下，看看有什么惊喜。

根据动态规划的定义，首先我们需要把原来的问题分解成了几个相似的子问题。但是，不同于斐波拉契数列的例子，这个如何分解原问题并不是那么一目了然。

原来的问题是求LIS(n)，现在我们需要找的就是LIS(n)和LIS(k)之间的关系1<=k<=n。通过肉眼观察一下：

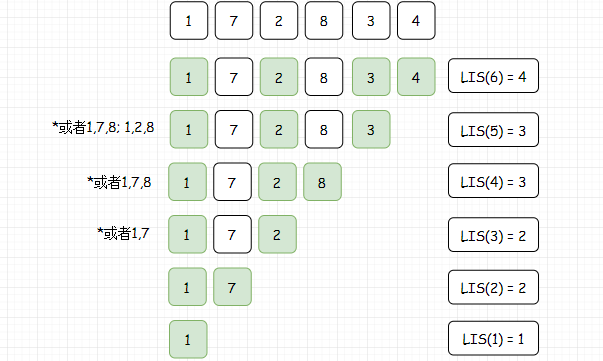
这里我们可以看到，LIS(K+1)要么等于LIS(K)，要么加了一。其实也很好理解，基本上就是，在前面所有的LIS种找到一个最长的LIS(i)，如果A(K)比这个找到LIS(i)的尾项A(i)要大，则LIS(K)=LIS(i)+1，否则LIS(K)=LIS(i)。

这样的话，我们就分解了原问题，并且找到了原问题和子问题之间的关系：

i是对应的最大LIS(i)。也就是说，计算LIS(n)需要计算之前所有的LIS(K)：

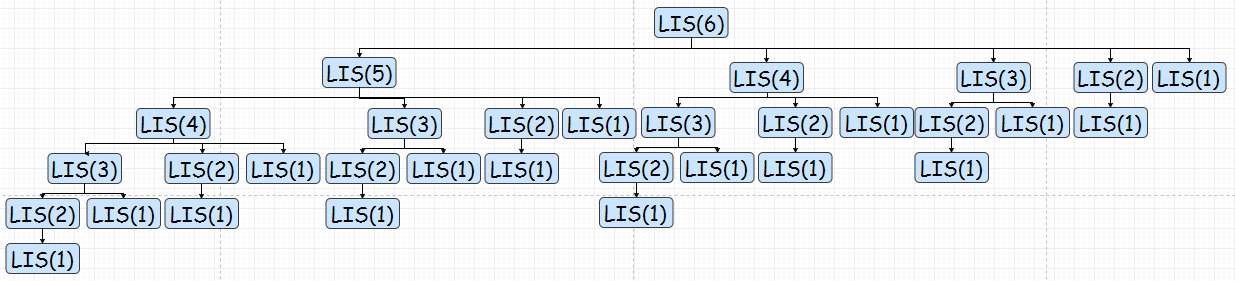
同理，我们可以储存子问题的结果，让每个子问题只被计算一次。需要计算的子问题就只剩下蓝色标出的部分了：

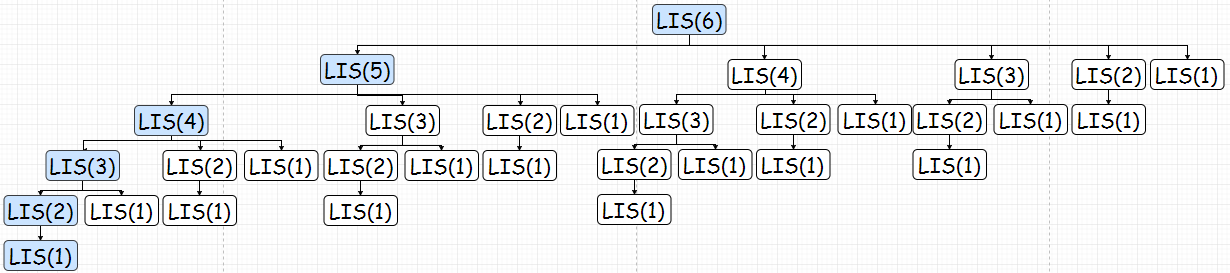
也就是（红色箭头表示调用了储存的数据，并未进行计算）：

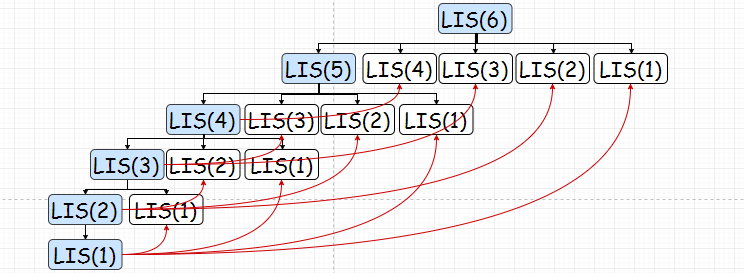
我们可以看到，采用了动态规划之后，时间复杂度大大降低了：纵轴方向的递归计算返回时间复杂度是O(n)，横轴方向每行求Max的时间复杂度是O(logn)，所以总共的时间复杂度就是O(nlogn)，远远小于暴力穷举法的O(2^n)。屌的一匹！

这就是动态规划的意义！在某些类型的问题中，动态规划通过巧妙的分治和记录子问题的解，可以给原本时间开销巨大的问题提供时间效率上大大优化的解决方案。

动态规划的三个特点都很重要，少了任何一个，都会有可能导致动态规划发挥不了应有的威力。比如在第一个斐波拉契数列的例子中，如果我们只是分解成了相似的子问题，但是并不储存子问题的解，那么最后那个算法的时间复杂度其实是指数级别的O(2^n)，反而比直观解法更慢了。同样的，动态规划只能优化一部分问题。比如最长递增子序列的暴力解法VS动态规划解法是O(n!) vs O(nlogn)，有很强的优化效果，但是斐波拉契数列的暴力解法VS动态规划解法是O(n) vs O(n)，动态规划并不能起到优化的效果。

在学生时代的时候，我一开始也一直对于动态规划这一部分比较困惑，主要大多数教材和讲解都运用了大量抽象的公式和不太容易理解的数学语言。这里，我希望借助视觉化算法的过程，以及尽量通俗的语言和例子，能让你大概了解到，动态规划到底是个啥？就Ok了。本题下很多答案都回答的很好，看了很多，受益匪浅。就像很多答主提到过的，动态规划之所以比较难以掌握，在于如何把原问题分解为相似的子问题，以及如何找到原问题和子问题之间的关系。这两点需要大量的练习和总结才能熟练运用。

最后，说一点题外话。@徐凯强 Andy 的最高票答案，回答的很好，也很有参考价值。但是他有一点是我不太喜欢的，就是他的答案里不停的强调动态规划的本质对问题状态的定义和状态转移方程的定义，而储存重叠子问题的解只是一种“技巧”，与动态规划的本质无关。这对很多人是有一定误导性的（我自己曾经就困扰了很久动态规划和分治法的区别到底是啥）。他的答案中，引用维基百科对于动态规划的定义的时候，不知是有心还是无意，他只节选了前半句：

dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.

但是，实际上，维基百科对于动规的定义里，还有更重要的后半句他漏掉了：

dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

Ref: Dynamic programming

也就是说，没有后面半句，只有前面半句，根本不能算是动态规划，只能算是分治法。储存重叠子问题的解，并不只是一个“花费空间来节省时间的技巧”，而就是动态规划的定义和核心之一。我不知道最高票答主是有意为了支持自己观点而故意断章取义了维基百科的对于动态规划的定义，还是无心而为之。我希望是后者。

　　很有意思的问题。以往见过许多教材，对动态规划（DP）的引入属于“奉天承运，皇帝诏曰”式：不给出一点引入，见面即拿出一大堆公式吓人；学生则死啃书本，然后突然顿悟。针对入门者的教材不应该是这样的。恰好我给入门者讲过四次DP入门，迭代出了一套比较靠谱的教学方法，所以今天跑过来献丑。

　　现在，我们试着自己来一步步“重新发明”DP。

　　先来看看生活中经常遇到的事吧——假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

　　依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

　　这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让w变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

　　但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：
　　15=1×11+4×1 （贪心策略使用了5张钞票）
　　15=3×5 （正确的策略，只用3张钞票）
　　为什么会这样呢？贪心策略错在了哪里？

　　鼠目寸光。
　　刚刚已经说过，贪心策略的纲领是：“尽量使接下来面对的w更小”。这样，贪心策略在w=15的局面时，会优先使用11来把w降到4；但是在这个问题中，凑出4的代价是很高的，必须使用4×1。如果使用了5，w会降为10，虽然没有4那么小，但是凑出10只需要两张5元。
　　在这里我们发现，贪心是一种只考虑眼前情况的策略。

　　那么，现在我们怎样才能避免鼠目寸光呢？

　　如果直接暴力枚举凑出w的方案，明显复杂度过高。太多种方法可以凑出w了，枚举它们的时间是不可承受的。我们现在来尝试找一下性质。

　　重新分析刚刚的例子。w=15时，我们如果取11，接下来就面对w=4的情况；如果取5，则接下来面对w=10的情况。我们发现这些问题都有相同的形式：“给定w，凑出w所用的最少钞票是多少张？”接下来，我们用f(n)来表示“凑出n所需的最少钞票数量”。

　　那么，如果我们取了11，最后的代价（用掉的钞票总数）是多少呢？
　　明显 ，它的意义是：利用11来凑出15，付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。
　　依次类推，马上可以知道：如果我们用5来凑出15，cost就是 。

　　那么，现在w=15的时候，我们该取那种钞票呢？当然是各种方案中，cost值最低的那一个！

　　- 取11：
　　- 取5：
　　- 取1：

　　显而易见，cost值最低的是取5的方案。我们通过上面三个式子，做出了正确的决策！

　　这给了我们一个至关重要的启示—— 只与 相关；更确切地说：

　　这个式子是非常激动人心的。我们要求出f(n)，只需要求出几个更小的f值；既然如此，我们从小到大把所有的f(i)求出来不就好了？注意一下边界情况即可。代码如下：

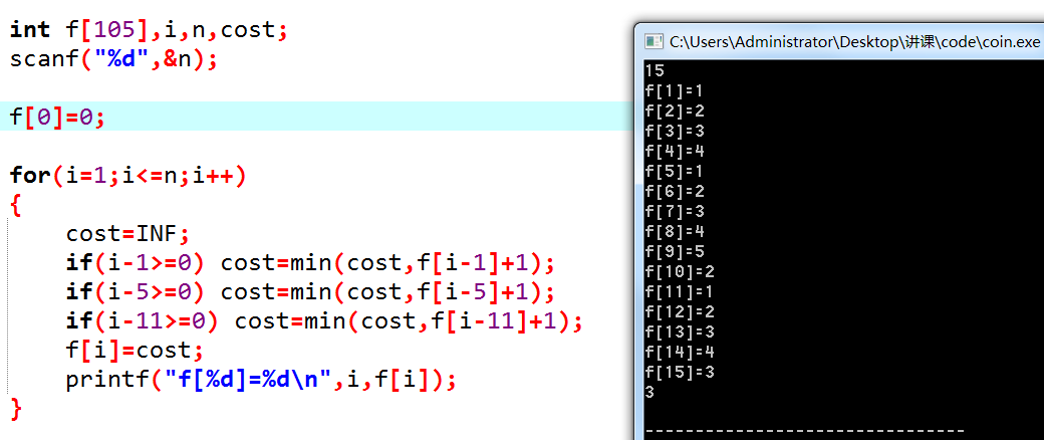
　　我们以 的复杂度解决了这个问题。现在回过头来，我们看看它的原理：

　　- 只与的值相关。
　　- 我们只关心 的值，不关心是怎么凑出w的。

　　这两个事实，保证了我们做法的正确性。它比起贪心策略，会分别算出取1、5、11的代价，从而做出一个正确决策，这样就避免掉了“鼠目寸光”！

　　它与暴力的区别在哪里？我们的暴力枚举了“使用的硬币”，然而这属于冗余信息。我们要的是答案，根本不关心这个答案是怎么凑出来的。譬如，要求出f(15)，只需要知道f(14),f(10),f(4)的值。其他信息并不需要。我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n).

　　我们能这样干，取决于问题的性质：求出f(n)，只需要知道几个更小的f(c)。我们将求解f(c)称作求解f(n)的“子问题”。

　　这就是DP（动态规划，dynamic programming）.

　　将一个问题拆成几个子问题，分别求解这些子问题，即可推断出大问题的解。

思考题：请稍微修改代码，输出我们凑出w的方案。

【无后效性】

　　一旦f(n)确定，“我们如何凑出f(n)”就再也用不着了。

　　要求出f(15)，只需要知道f(14),f(10),f(4)的值，而f(14),f(10),f(4)是如何算出来的，对之后的问题没有影响。

　　“未来与过去无关”，这就是无后效性。

　　（严格定义：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。）

【最优子结构】

　　回顾我们对f(n)的定义：我们记“凑出n所需的最少钞票数量”为f(n).

　　f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解，我们即可算出w=15的最优解。

　　大问题的最优解可以由小问题的最优解推出，这个性质叫做“最优子结构性质”。

　　引入这两个概念之后，我们如何判断一个问题能否使用DP解决呢？

　　能将大问题拆成几个小问题，且满足无后效性、最优子结构性质。

　　问题很简单：给定一个城市的地图，所有的道路都是单行道，而且不会构成环。每条道路都有过路费，问您从S点到T点花费的最少费用。

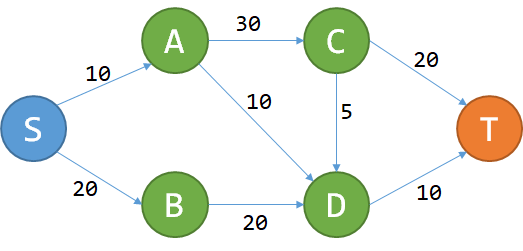
　　这个问题能用DP解决吗？我们先试着记从S到P的最少费用为f(P).
　　想要到T，要么经过C，要么经过D。从而.

　　好像看起来可以DP。现在我们检验刚刚那两个性质：
　　- 无后效性：对于点P，一旦f(P)确定，以后就只关心f(P)的值，不关心怎么去的。
　　- 最优子结构：对于P，我们当然只关心到P的最小费用，即f(P)。如果我们从S走到T是 ，那肯定S走到Q的最优路径是 。对一条最优的路径而言，从S走到沿途上所有的点（子问题）的最优路径，都是这条大路的一部分。这个问题的最优子结构性质是显然的。

　　既然这两个性质都满足，那么本题可以DP。式子明显为：

　　其中R为有路通到P的所有的点， 为R到P的过路费。

　　代码实现也很简单，拓扑排序即可。

【DP的核心思想】

　　DP为什么会快？
　　无论是DP还是暴力，我们的算法都是在可能解空间内，寻找最优解。

　　来看钞票问题。暴力做法是枚举所有的可能解，这是最大的可能解空间。
　　DP是枚举有希望成为答案的解。这个空间比暴力的小得多。

　　也就是说：DP自带剪枝。

　　DP舍弃了一大堆不可能成为最优解的答案。譬如：
　　15=5+5+5 被考虑了。
　　15=5+5+1+1+1+1+1 从来没有考虑过，因为这不可能成为最优解。

　　从而我们可以得到DP的核心思想：尽量缩小可能解空间。

　　在暴力算法中，可能解空间往往是指数级的大小；如果我们采用DP，那么有可能把解空间的大小降到多项式级。

　　一般来说，解空间越小，寻找解就越快。这样就完成了优化。

【DP的操作过程】

　　一言以蔽之：大事化小，小事化了。

　　将一个大问题转化成几个小问题；
　　求解小问题；
　　推出大问题的解。

【如何设计DP算法】

　　下面介绍比较通用的设计DP算法的步骤。

　　首先，把我们面对的局面表示为x。这一步称为设计状态。
　　对于状态x，记我们要求出的答案(e.g. 最小费用)为f(x).我们的目标是求出f(T).
找出f(x)与哪些局面有关（记为p），写出一个式子（称为状态转移方程），通过f(p)来推出f(x).

【DP三连】

　　设计DP算法，往往可以遵循DP三连：

　　我是谁？ ——设计状态，表示局面
　　我从哪里来？
　　我要到哪里去？ ——设计转移

　　设计状态是DP的基础。接下来的设计转移，有两种方式：一种是考虑我从哪里来（本文之前提到的两个例子，都是在考虑“我从哪里来”）；另一种是考虑我到哪里去，这常见于求出f(x)之后，更新能从x走到的一些解。这种DP也是不少的，我们以后会遇到。

　　总而言之，“我从哪里来”和“我要到哪里去”只需要考虑清楚其中一个，就能设计出状态转移方程，从而写代码求解问题。前者又称pull型的转移，后者又称push型的转移。（这两个词是 @阮止雨 妹妹告诉我的，不知道源出处在哪）

思考题：如何把钞票问题的代码改写成“我到哪里去”的形式？
提示：求出f(x)之后，更新f(x+1),f(x+5),f(x+11).

　　扯了这么多形而上的内容，还是做一道例题吧。

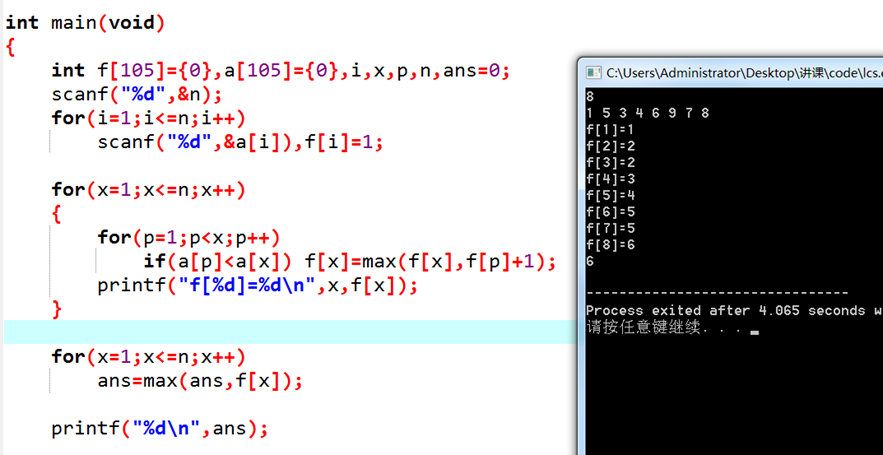
　　最长上升子序列（LIS）问题：给定长度为n的序列a，从a中抽取出一个子序列，这个子序列需要单调递增。问最长的上升子序列（LIS）的长度。
　　e.g. 1,5,3,4,6,9,7,8的LIS为1,3,4,6,7,8，长度为6。

　　如何设计状态（我是谁）？

　　我们记 为以 结尾的LIS长度，那么答案就是 .

　　状态x从哪里推过来（我从哪里来）？

　　考虑比x小的每一个p：如果 ，那么f(x)可以取f(p)+1.
　　解释：我们把 接在 的后面，肯定能构造一个以 结尾的上升子序列，长度比以 结尾的LIS大1.那么，我们可以写出状态转移方程了：

　　至此解决问题。两层for循环，复杂度 .

　　从这三个例题中可以看出，DP是一种思想，一种“大事化小，小事化了”的思想。带着这种思想，DP将会成为我们解决问题的利器。

　　最后，我们一起念一遍DP三连吧——我是谁？我从哪里来？我要到哪里去？

如果读者有兴趣，可以试着完成下面几个习题：

一、请采取一些优化手段，以 的复杂度解决LIS问题。

提示：可以参考这篇博客 Junior Dynamic Programming--动态规划初步·各种子序列问题

二、“按顺序递推”和“记忆化搜索”是实现DP的两种方式。请查阅资料，简单描述“记忆化搜索”是什么。并采用记忆化搜索写出钞票问题的代码，然后完成P1541 乌龟棋 - 洛谷 。

三、01背包问题是一种常见的DP模型。请完成P1048 采药 - 洛谷。

谢谢您看完本文 ?(? ? ?ω? ? ?)?

2019.3.3

之前写过一篇入门动态规划地文章，文章中给出了动态规划地套路和优化方案，在知乎收获了不少赞，也收到挺多人感谢

这里分享给需要的人，正文如下：

之前写过一篇入门动态规划地文章，文章中给出了动态规划地套路和优化方案，在知乎收获了不少赞，也收到挺多人感谢动态规划难吗？说实话，我觉得很难，特别是对于初学者来说，我当时入门动态规划的时候，是看 0-1 背包问题，当时真的是一脸懵逼。后来，我遇到动态规划的题，看的懂答案，但就是自己不会做，不知道怎么下手。就像做递归的题，看的懂答案，但下不了手，关于递归的，我之前也写过一篇套路的文章，如果对递归不大懂的，强烈建议看一看：为什么你学不会递归，告别递归，谈谈我的经验

对于动态规划，春招秋招时好多题都会用到动态规划，一气之下，再 leetcode 连续刷了几十道题

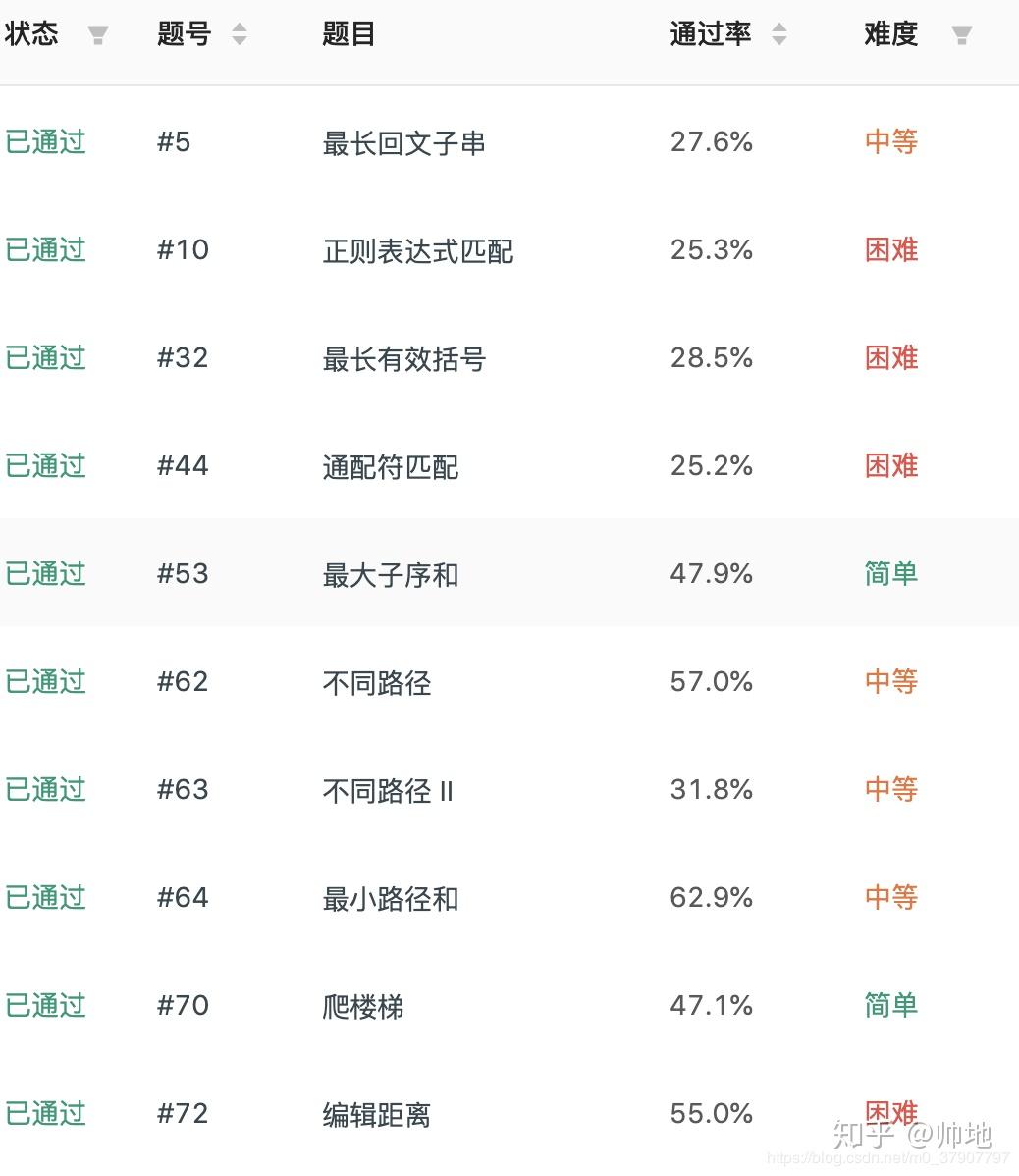
之后，豁然开朗 ，感觉动态规划也不是很难，今天，我就来跟大家讲一讲，我是怎么做动态规划的题的，以及从中学到的一些套路。相信你看完一定有所收获

如果你对动态规划感兴趣，或者你看的懂动态规划，但却不知道怎么下手，那么我建议你好好看以下，这篇文章的写法，和之前那篇讲递归的写法，是差不多一样的，将会举大量的例子。如果一次性看不完，建议收藏，同时别忘了素质三连。

为了兼顾初学者，我会从最简单的题讲起，后面会越来越难，最后面还会讲解，该如何优化。因为 80% 的动规都是可以进行优化的。不过我得说，如果你连动态规划是什么都没听过，可能这篇文章你也会压力山大。

动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤，

如果你听不懂，也没关系，下面会有很多例题讲解，估计你就懂了。之所以不配合例题来讲这些步骤，也是为了怕你们脑袋乱了

第一步骤：定义数组元素的含义，上面说了，我们会用一个数组，来保存历史数组，假设用一维数组 dp[]吧。这个时候有一个非常非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i]是代表什么意思？

第二步骤：找出数组元素之间的关系式，我觉得动态规划，还是有一点类似于我们高中学习时的归纳法的，当我们要计算 dp[n]时，是可以利用 dp[n-1]，dp[n-2].....dp[1]，来推出 dp[n]的，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n]=dp[n-1]+ dp[n-2]，这个就是他们的关系式了。而这一步，也是最难的一步，后面我会讲几种类型的题来说。

学过动态规划的可能都经常听到最优子结构，把大的问题拆分成小的问题，说实话，最开始的时候，我是对最优子结构一梦懵逼的。估计你们也听多了，所以这一次，我将换一种形式来讲，不再是各种子问题，各种最优子结构。所以大佬可别喷我再乱讲，因为我说了，这是我自己平时做题的套路。

第三步骤：找出初始值。学过数学归纳法的都知道，虽然我们知道了数组元素之间的关系式，例如 dp[n]=dp[n-1]+ dp[n-2]，我们可以通过 dp[n-1]和 dp[n-2]来计算 dp[n]，但是，我们得知道初始值啊，例如一直推下去的话，会由 dp[3]=dp[2]+ dp[1]。而 dp[2]和 dp[1]是不能再分解的了，所以我们必须要能够直接获得 dp[2]和 dp[1]的值，而这，就是所谓的初始值。

由了初始值，并且有了数组元素之间的关系式，那么我们就可以得到 dp[n]的值了，而 dp[n]的含义是由你来定义的，你想求什么，就定义它是什么，这样，这道题也就解出来了。

不懂？没事，我们来看三四道例题，我讲严格按这个步骤来给大家讲解。

问题描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

按我上面的步骤说的，首先我们来定义 dp[i]的含义，我们的问题是要求青蛙跳上 n 级的台阶总共由多少种跳法，那我们就定义 dp[i]的含义为：跳上一个 i 级的台阶总共有 dp[i]种跳法。这样，如果我们能够算出 dp[n]，不就是我们要求的答案吗？所以第一步定义完成。

我们的目的是要求 dp[n]，动态规划的题，如你们经常听说的那样，就是把一个规模比较大的问题分成几个规模比较小的问题，然后由小的问题推导出大的问题。也就是说，dp[n]的规模为 n，比它规模小的是 n-1, n-2, n-3.... 也就是说，dp[n]一定会和 dp[n-1], dp[n-2]....存在某种关系的。我们要找出他们的关系。

那么问题来了，怎么找？

这个怎么找，是最核心最难的一个，我们必须回到问题本身来了，来寻找他们的关系式，dp[n]究竟会等于什么呢？

对于这道题，由于情况可以选择跳一级，也可以选择跳两级，所以青蛙到达第 n 级的台阶有两种方式

一种是从第 n-1 级跳上来

一种是从第 n-2 级跳上来

由于我们是要算所有可能的跳法的，所以有 dp[n]=dp[n-1]+ dp[n-2]。

当 n=1 时，dp[1]=dp[0]+ dp[-1]，而我们是数组是不允许下标为负数的，所以对于 dp[1]，我们必须要直接给出它的数值，相当于初始值，显然，dp[1]=1。一样，dp[0]=0（0 个台阶，有人说是0种跳法，有人说是1种，我们暂时当作0种处理吧，不过无论哪种，都不影响问题都思路哈）。于是得出初始值：

dp[0]=0. dp[1]=1. 即 n <=1时，dp[n]=n

三个步骤都做出来了，那么我们就来写代码吧，代码会详细注释滴。

int f( int n ){
    if(n <= 1)
    return n;
    // 先创建一个数组来保存历史数据
    int[] dp = new int[n+1];
    // 给出初始值
    dp[0] = 0;
    dp[1] = 1;
    // 通过关系式来计算出 dp[n]
    for(int i = 2; i <= n; i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    // 把最终结果返回
    return dp[n];
}

大家先想以下，你觉得，上面的代码有没有问题？

答是有问题的，还是错的，错在对初始值的寻找不够严谨，这也是我故意这样弄的，意在告诉你们，关于初始值的严谨性。例如对于上面的题，当 n=2 时，dp[2]=dp[1]+ dp[0]=1。这显然是错误的，你可以模拟一下，应该是 dp[2]=2。

也就是说，在寻找初始值的时候，一定要注意不要找漏了，dp[2]也算是一个初始值，不能通过公式计算得出。有人可能会说，我想不到怎么办？这个很好办，多做几道题就可以了。

下面我再列举三道不同的例题，并且，再在未来的文章中，我也会持续按照这个步骤，给大家找几道有难度且类型不同的题。下面这几道例题，不会讲的特性详细哈。实际上 ，上面的一维数组是可以把空间优化成更小的，不过我们现在先不讲优化的事，下面的题也是，不讲优化版本。

我做了几十道 DP 的算法题，可以说，80% 的题，都是要用二维数组的，所以下面的题主要以二维数组为主，当然有人可能会说，要用一维还是二维，我怎么知道？这个问题不大，接着往下看。

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

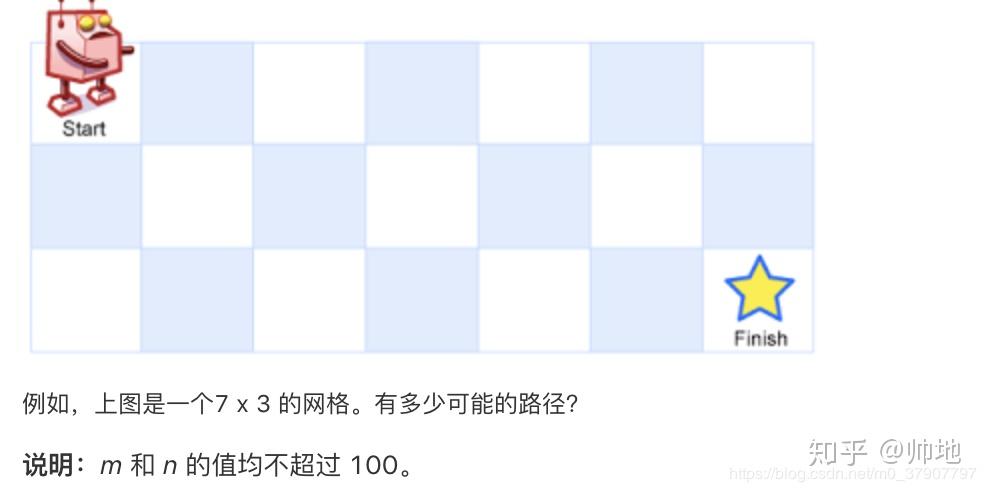
这是 leetcode 的 62 号题：https://leetcode-cn.com/problems/unique-paths/

还是老样子，三个步骤来解决。

由于我们的目的是从左上角到右下角一共有多少种路径，那我们就定义 dp[i][j]的含义为：当机器人从左上角走到(i, j) 这个位置时，一共有 dp[i][j]种路径。那么，dp[m-1][n-1]就是我们要的答案了。

注意，这个网格相当于一个二维数组，数组是从下标为 0 开始算起的，所以 右下角的位置是 (m-1, n - 1)，所以 dp[m-1][n-1]就是我们要找的答案。

想象以下，机器人要怎么样才能到达 (i, j) 这个位置？由于机器人可以向下走或者向右走，所以有两种方式到达

一种是从 (i-1, j) 这个位置走一步到达

一种是从(i, j - 1) 这个位置走一步到达

因为是计算所有可能的步骤，所以是把所有可能走的路径都加起来，所以关系式是 dp[i][j]=dp[i-1][j]+ dp[i][j-1]。

显然，当 dp[i][j]中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0][0….n-1]和所有的 dp[0….m-1][0]。这个还是非常容易计算的，相当于计算机图中的最上面一行和左边一列。因此初始值如下：

dp[0][0….n-1]=1; // 相当于最上面一行，机器人只能一直往左走

dp[0…m-1][0]=1; // 相当于最左面一列，机器人只能一直往下走

三个步骤都写出来了，直接看代码

public static int uniquePaths(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
    // 初始化
    for(int i = 0; i < m; i++){
      dp[i][0] = 1;
    }
    for(int i = 0; i < n; i++){
      dp[0][i] = 1;
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的，不过这里先不讲

写到这里，有点累了，，但还是得写下去，所以看的小伙伴，你们可得继续看呀。下面这道题也不难，比上面的难一丢丢，不过也是非常类似

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

举例：
输入:
arr = [
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

和上面的差不多，不过是算最优路径和，这是 leetcode 的第64题：https://leetcode-cn.com/problems/minimum-path-sum/

还是老样子，可能有些人都看烦了，哈哈，但我还是要按照步骤来写，让那些不大懂的加深理解。有人可能觉得，这些题太简单了吧，别慌，小白先入门，这些属于 medium 级别的，后面在给几道 hard 级别的。

由于我们的目的是从左上角到右下角，最小路径和是多少，那我们就定义 dp[i][j]的含义为：当机器人从左上角走到(i, j) 这个位置时，最下的路径和是 dp[i][j]。那么，dp[m-1][n-1]就是我们要的答案了。

注意，这个网格相当于一个二维数组，数组是从下标为 0 开始算起的，所以 由下角的位置是 (m-1, n - 1)，所以 dp[m-1][n-1]就是我们要走的答案。

想象以下，机器人要怎么样才能到达 (i, j) 这个位置？由于机器人可以向下走或者向右走，所以有两种方式到达

一种是从 (i-1, j) 这个位置走一步到达

一种是从(i, j - 1) 这个位置走一步到达

不过这次不是计算所有可能路径，而是计算哪一个路径和是最小的，那么我们要从这两种方式中，选择一种，使得dp[i][j]的值是最小的，显然有

dp[i] [j] = min(dp[i-1][j]，dp[i][j-1]) + arr[i][j];// arr[i][j] 表示网格种的值

显然，当 dp[i][j]中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0][0….n-1]和所有的 dp[0….m-1][0]。这个还是非常容易计算的，相当于计算机图中的最上面一行和左边一列。因此初始值如下：

dp[0][j]=arr[0][j]+ dp[0][j-1]; // 相当于最上面一行，机器人只能一直往左走

dp[i][0]=arr[i][0]+ dp[i][0]; // 相当于最左面一列，机器人只能一直往下走

public static int uniquePaths(int[][] arr) {
    int m = arr.length;
    int n = arr[0].length;
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
    // 初始化
    dp[0][0] = arr[0][0];
    // 初始化最左边的列
    for(int i = 1; i < m; i++){
      dp[i][0] = dp[i-1][0] + arr[i][0];
    }
    // 初始化最上边的行
    for(int i = 1; i < n; i++){
      dp[0][i] = dp[0][i-1] + arr[0][i];
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + arr[i][j];
        }
    }
    return dp[m-1][n-1];
}

O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的，不过这里先不讲

这次给的这道题比上面的难一些，在 leetcdoe 的定位是 hard 级别。好像是 leetcode 的第 72 号题。

问题描述

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符 删除一个字符 替换一个字符

示例：
输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

解答

还是老样子，按照上面三个步骤来，并且我这里可以告诉你，90% 的字符串问题都可以用动态规划解决，并且90%是采用二维数组。

由于我们的目的求将 word1 转换成 word2 所使用的最少操作数 。那我们就定义 dp[i][j]的含义为：当字符串 word1 的长度为 i，字符串 word2 的长度为 j 时，将 word1 转化为 word2 所使用的最少操作次数为 dp[i][j]。

有时候，数组的含义并不容易找，所以还是那句话，我给你们一个套路，剩下的还得看你们去领悟。

接下来我们就要找 dp[i][j]元素之间的关系了，比起其他题，这道题相对比较难找一点，但是，不管多难找，大部分情况下，dp[i][j]和 dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]肯定存在某种关系。因为我们的目标就是，**从规模小的，通过一些操作，推导出规模大的。对于这道题，我们可以对 word1 进行三种操作

插入一个字符 删除一个字符 替换一个字符

由于我们是要让操作的次数最小，所以我们要寻找最佳操作。那么有如下关系式：

一、如果我们 word1[i]与 word2[j]相等，这个时候不需要进行任何操作，显然有 dp[i][j]=dp[i-1][j-1]。（别忘了 dp[i][j]的含义哈）。

二、如果我们 word1[i]与 word2[j]不相等，这个时候我们就必须进行调整，而调整的操作有 3 种，我们要选择一种。三种操作对应的关系试如下（注意字符串与字符的区别）：

（1）、如果把字符 word1[i]替换成与 word2[j]相等，则有 dp[i][j]=dp[i-1][j-1]+ 1;

（2）、如果在字符串 word1末尾插入一个与 word2[j]相等的字符，则有 dp[i][j]=dp[i][j-1]+ 1;

（3）、如果把字符 word1[i]删除，则有 dp[i][j]=dp[i-1][j]+ 1;

那么我们应该选择一种操作，使得 dp[i][j]的值最小，显然有

dp[i][j]=min(dp[i-1][j-1]，dp[i][j-1]，dp[[i-1][j]]) + 1;

于是，我们的关系式就推出来了，

显然，当 dp[i][j]中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0][0….n]和所有的 dp[0….m][0]。这个还是非常容易计算的，因为当有一个字符串的长度为 0 时，转化为另外一个字符串，那就只能一直进行插入或者删除操作了。

public int minDistance(String word1, String word2) {
    int n1 = word1.length();
    int n2 = word2.length();
    int[][] dp = new int[n1 + 1][n2 + 1];
    // dp[0][0...n2]的初始值
    for (int j = 1; j <= n2; j++) 
        dp[0][j] = dp[0][j - 1] + 1;
    // dp[0...n1][0]的初始值
    for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
        // 通过公式推出 dp[n1][n2]
    for (int i = 1; i <= n1; i++) {
        for (int j = 1; j <= n2; j++) {
            // 如果 word1[i]与 word2[j]相等。第 i 个字符对应下标是 i-1
            if (word1.charAt(i - 1) == word2.charAt(j - 1)){
                p[i][j] = dp[i - 1][j - 1];
            }else {
               dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
            }         
        }
    }
    return dp[n1][n2];  
}

最后说下，如果你要练习，可以去 leetcode，选择动态规划专题，然后连续刷几十道，保证你以后再也不怕动态规划了。当然，遇到很难的，咱还是得挂。

Leetcode 动态规划直达：https://leetcode-cn.com/tag/dynamic-programming/

前两天写一篇长达 8000 子的关于动态规划的文章告别动态规划，连刷40道动规算法题，我总结了动规的套路

这篇文章更多讲解我平时做题的套路，不过由于篇幅过长，举了 4 个案例之后，没有讲解优化，今天这篇文章就来讲解下，对动态规划的优化如何下手，并且以前几天那篇文章的题作为例子直接讲优化，如果没看过的建议看一下（不看也行，我会直接给出题目以及没有优化前的代码）：告别动态规划，连刷40道动规算法题，我总结了动规的套路

没错，80% 的动态规划题都可以画图，其中 80% 的题都可以通过画图一下子知道怎么优化，当然，DP 也有一些很难的题，想优化可没那么容易，不过，今天我要讲的，是属于不怎么难，且最常见，面试笔试最经常考的难度的题。

下面我们直接通过三道题目来讲解优化，你会发现，这些题，优化过后，代码只有细微的改变，你只要会一两道，可以说是会了 80% 的题。

上次那个青蛙跳台阶的 dp 题是可以把空间复杂度 O( n) 优化成 O(1)，本来打算从这道题讲起的，但想了下，想要学习 dp 优化的感觉至少都是 小小大佬了，所以就不讲了，就从二维数组的 dp 讲起。

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

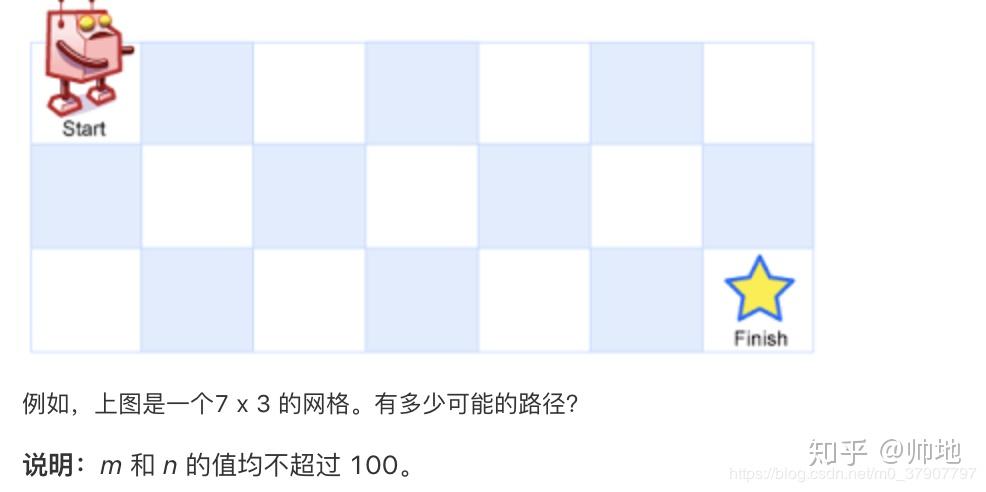
这是 leetcode 的 62 号题：https://leetcode-cn.com/problems/unique-paths/

这道题的 dp 转移公式是 dp[i][j]=dp[i-1][j]+ dp[i][j-1]，代码如下

不懂的看我之前文章：告别动态规划，连刷40道动规算法题，我总结了动规的套路

public static int uniquePaths(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
    // 初始化
    for(int i = 0; i < m; i++){
      dp[i][0] = 1;
    }
    for(int i = 0; i < n; i++){
      dp[0][i] = 1;
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

这种做法的空间复杂度是 O(n * m)，下面我们来讲解如何优化成 O(n)。

dp[i][j]是一个二维矩阵，我们来画个二维矩阵的图，对矩阵进行初始化

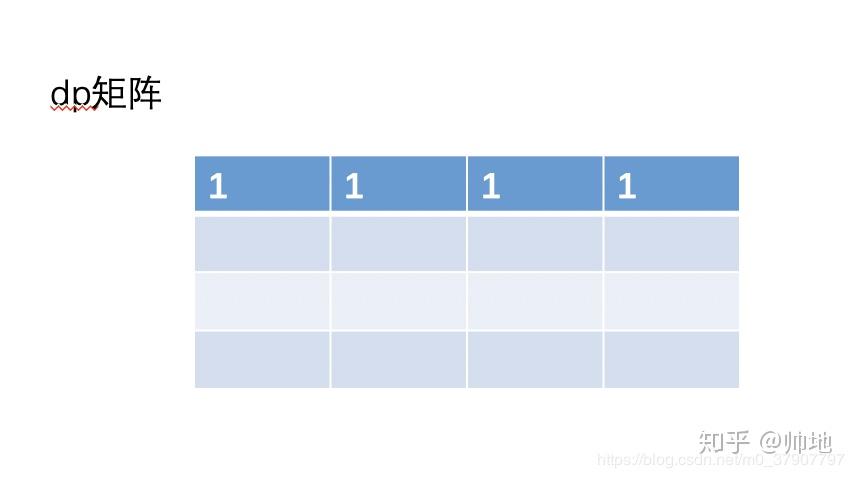
然后根据公式 dp[i][j]=dp[i-1][j]+ dp[i][j-1]来填充矩阵的其他值。下面我们先填充第二行的值。

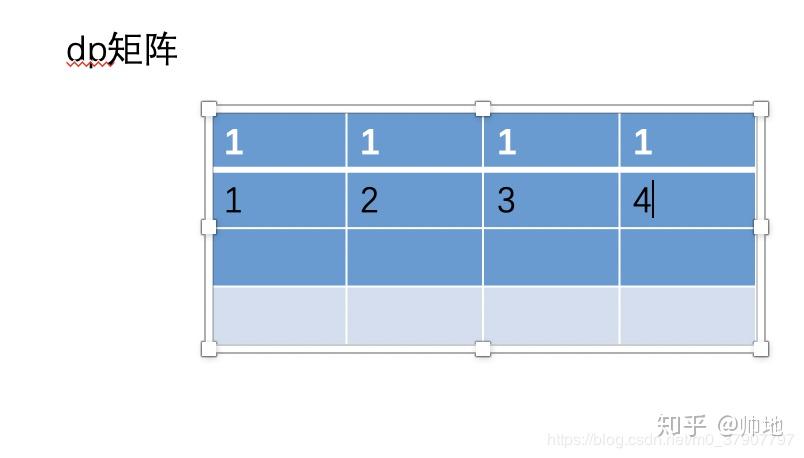
大家想一个问题，当我们要填充第三行的值的时候，我们需要用到第一行的值吗？答是不需要的，不行你试试，当你要填充第三，第四....第 n 行的时候，第一行的值永远不会用到，只要填充第二行的值时会用到。

根据公式 dp[i][j]=dp[i-1][j]+ dp[i][j-1]，我们可以知道，当我们要计算第 i 行的值时，除了会用到第 i - 1 行外，其他第 1 至 第 i-2 行的值我们都是不需要用到的，也就是说，对于那部分用不到的值我们还有必要保存他们吗？

答是没必要，我们只需要用一个一维的 dp[]来保存一行的历史记录就可以了。然后在计算机的过程中，不断着更新 dp[]的值。单说估计你可能不好理解，下面我就手把手来演示下这个过程。

1、刚开始初始化第一行，此时 dp[0..n-1]的值就是第一行的值。

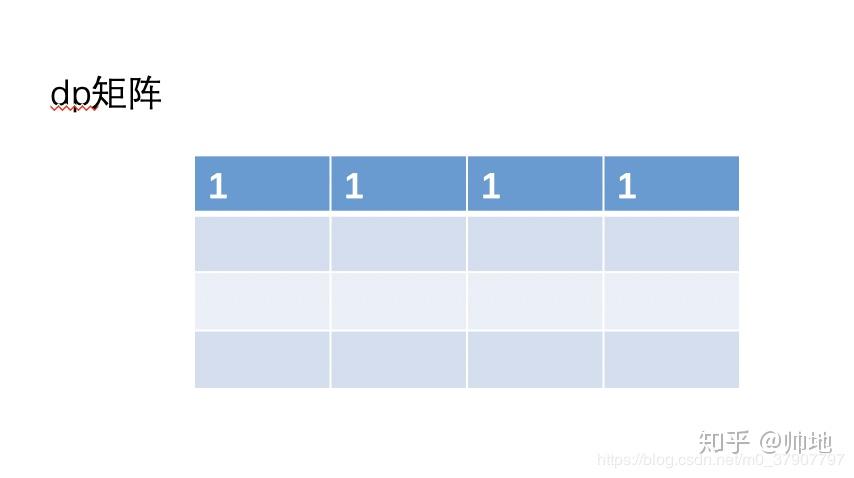
2、接着我们来一边填充第二行的值一边更新 dp[i]的值，一边把第一行的值抛弃掉。

为了方便描述，下面我们用arr (i，j）表示矩阵中第 i 行 第 j 列的值。从 0 开始哈，就是说有第 0 行。

（1）、显然，矩阵(1, 0) 的值相当于以往的初始化值，为 1。然后这个时候矩阵 (0，0）的值不在需要保存了，因为再也用不到了。

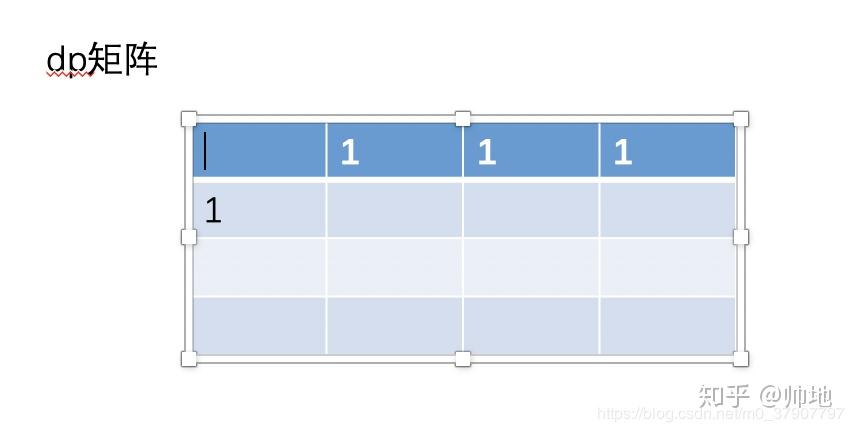
这个时候，我们也要跟着更新 dp[0]的值了，刚开始 dp[0]=(0, 0)，现在更新为 dp[0]=(1, 0)。

（2）、接着继续更新 (1, 1) 的值，根据之前的公式 （i, j)=(i-1, j) + (i, j- 1)。即 （1，1）=（0，1）+（1，0）=2。

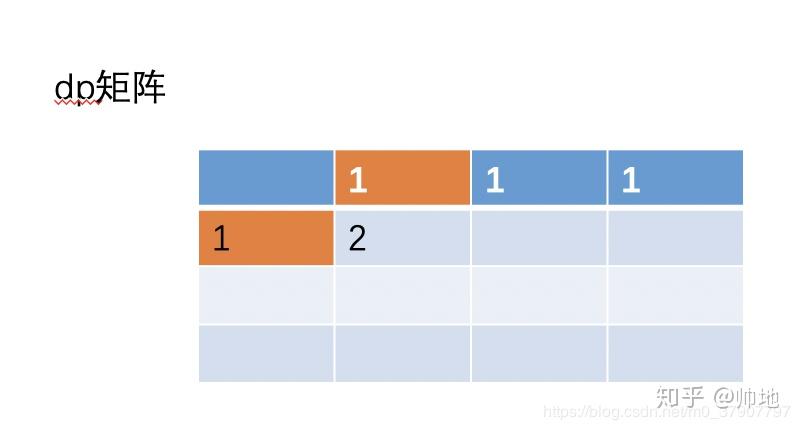
大家看图，以往的二维的时候， dp[i][j]=dp[i-1][j]+ dp[i][j-1]。现在转化成一维，不就是 dp[i]=dp[i]+ dp[i-1] 吗？

即 dp[1]=dp[1]+ dp[0]，而且还动态帮我们更新了 dp[1]的值。因为刚开始 dp[i]的保存第一行的值的，现在更新为保存第二行的值。

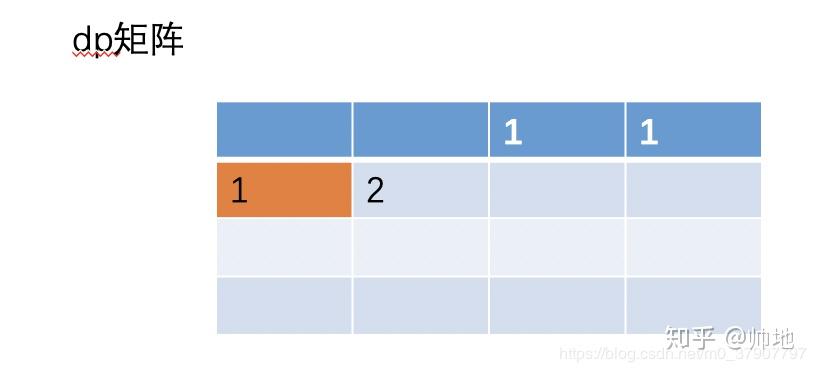
(3)、同样的道理，按照这样的模式一直来计算第二行的值，顺便把第一行的值抛弃掉，结果如下

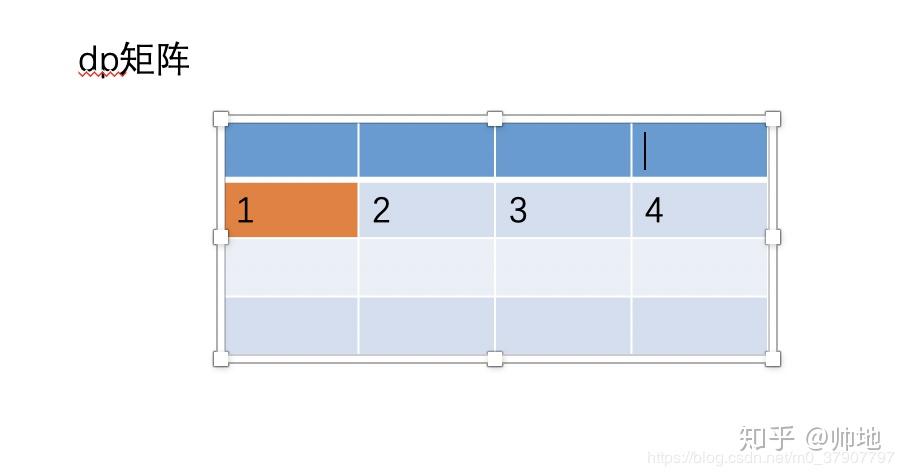
此时，dp[i]将完全保存着第二行的值，并且我们可以推导出公式

dp[i]=dp[i-1]+ dp[i]

dp[i-1]相当于之前的 dp[i-1][j]，dp[i]相当于之前的 dp[i][j-1]。

于是按照这个公式不停着填充到最后一行，结果如下：

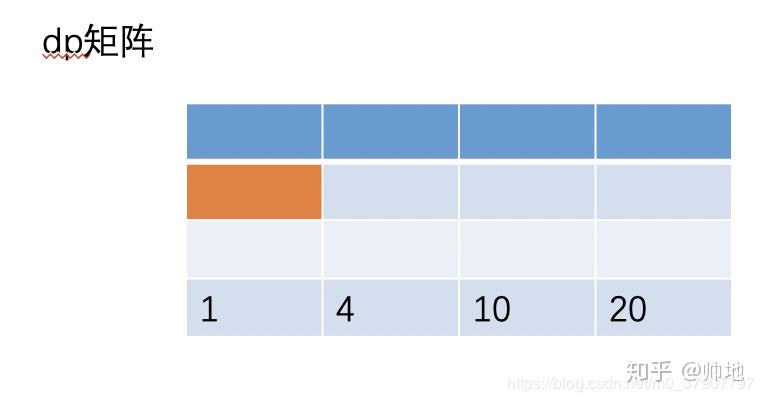
最后 dp[n-1]就是我们要求的结果了。所以优化之后，代码如下：

public static int uniquePaths(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[] dp = new int[n]; // 
    // 初始化
    for(int i = 0; i < n; i++){
      dp[i] = 1;
    }

        // 公式：dp[i]=dp[i-1]+ dp[i]
    for (int i = 1; i < m; i++) {
        // 第 i 行第 0 列的初始值
        dp[0] = 1;
        for (int j = 1; j < n; j++) {
            dp[j] = dp[j-1] + dp[j];
        }
    }
    return dp[n-1];
}

接着我们来看昨天的另外一道题，就是编辑矩阵，这道题的优化和这一道有一点点的不同，上面这道 dp[i][j]依赖于 dp[i-1][j]和 dp[i][j-1]。而还有一种情况就是 dp[i][j]依赖于 dp[i-1][j]，dp[i-1][j-1]和 dp[i][j-1]。

问题描述

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符 删除一个字符 替换一个字符

示例：
输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

解答

昨天的代码如下所示，不懂的记得看之前的文章哈：告别动态规划，连刷40道动规算法题，我总结了动规的套路

public int minDistance(String word1, String word2) {
    int n1 = word1.length();
    int n2 = word2.length();
    int[][] dp = new int[n1 + 1][n2 + 1];
    // dp[0][0...n2]的初始值
    for (int j = 1; j <= n2; j++) 
        dp[0][j] = dp[0][j - 1] + 1;
    // dp[0...n1][0]的初始值
    for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
        // 通过公式推出 dp[n1][n2]
    for (int i = 1; i <= n1; i++) {
        for (int j = 1; j <= n2; j++) {
            // 如果 word1[i]与 word2[j]相等。第 i 个字符对应下标是 i-1
            if (word1.charAt(i - 1) == word2.charAt(j - 1)){
                p[i][j] = dp[i - 1][j - 1];
            }else {
               dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
            }         
        }
    }
    return dp[n1][n2];  
}

没有优化之间的空间复杂度为 O(n*m)

大家可以自己动手做下，按照上面的那个模式，你会优化吗？

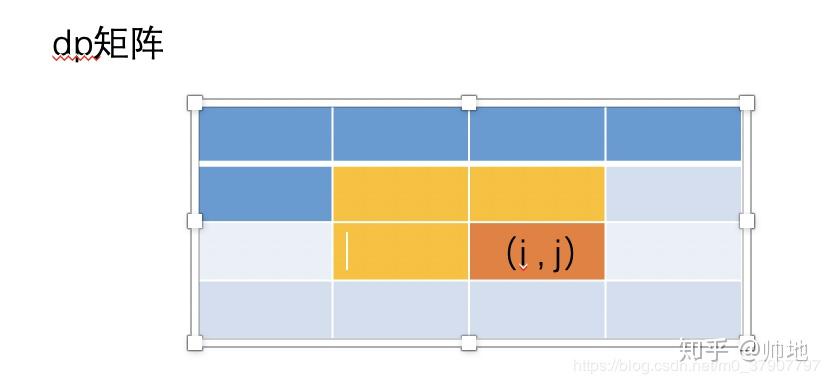
对于这道题其实也是一样的，如果要计算 第 i 行的值，我们最多只依赖第 i-1 行的值，不需要用到第 i-2 行及其以前的值，所以一样可以采用一维 dp 来处理的。

不过这个时候要注意，在上面的例子中，我们每次更新完 (i, j) 的值之后，就会把 (i, j-1) 的值抛弃，也就是说之前是一边更新 dp[i]的值，一边把 dp[i]的旧值抛弃的，不过在这道题中则不可以，因为我们还需要用到它。

哎呀，直接举例子看图吧，文字绕来绕去估计会绕晕你们。当我们要计算图中 (i,j) 的值的时候，在案例1 中，我们值需要用到 (i-1, j) 和 (i, j-1)。（看图中方格的颜色）

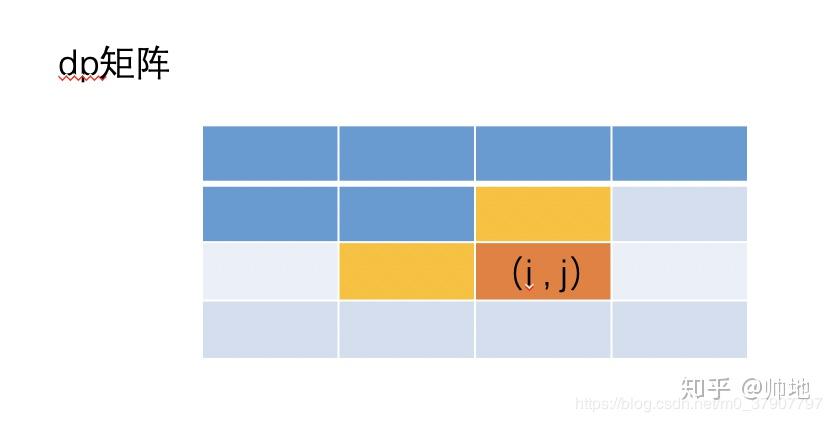
不过这道题中，我们还需要用到 （i-1, j-1) 这个值（但是这个值在以往的案例1 中，它会被抛弃掉）

所以呢，对于这道题，我们还需要一个额外的变量 pre 来时刻保存 (i-1,j-1) 的值。推导公式就可以从二维的

dp[i][j]=min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1

转化为一维的

dp[i]=min(dp[i-1], pre, dp[i]) + 1。

所以呢，案例2 其实和案例1 差别不大，就是多了个变量来临时保存。最终代码如下（但是初学者话，代码也没那么好写）

public int minDistance(String word1, String word2) {
    int n1 = word1.length();
    int n2 = word2.length();
    int[] dp = new int[n2 + 1];
    // dp[0...n2]的初始值
    for (int j = 0; j <= n2; j++) 
        dp[j] = j;
    // dp[j]=min(dp[j-1], pre, dp[j]) + 1
    for (int i = 1; i <= n1; i++) {
        int temp = dp[0];
        // 相当于初始化
        dp[0] = i;
        for (int j = 1; j <= n2; j++) {
            // pre 相当于之前的 dp[i-1][j-1]
            int pre = temp;
            temp = dp[j];
            // 如果 word1[i]与 word2[j]相等。第 i 个字符对应下标是 i-1
            if (word1.charAt(i - 1) == word2.charAt(j - 1)){
                dp[j] = pre;
            }else {
               dp[j] = Math.min(Math.min(dp[j - 1], pre), dp[j]) + 1;
            } 
            // 保存要被抛弃的值       
        }
    }
    return dp[n2]; 
}

上面的这些题，基本都是不怎么难的入门题，除了最后一道相对难一点。并且基本 80% 的二维矩阵 dp 都可以像上面的方法一样优化成 一维矩阵的 dp，核心就是要画图，看他们的值依赖，当然，还有很多其他比较难的优化，但是，我遇到的题中，大部分都是我上面这种类型的优化。后面如何遇到其他的，我会作为案例来讲，今天就先讲最普遍最通用的优化方案。记住，画二维 dp 的矩阵图，然后看元素之间的值依赖，然后就可以很清晰着知道该如何优化了。

在之后的文章中，我也会按照这个步骤，在给大家讲四五道动态规划 hard 级别的题，会放在每天推文的第二条给大家学习。如果觉得有收获，不放三连走起来（点赞、感谢、分享），嘻嘻。

最后，我把自己的原创精华文章整理成了一本电子书，共 630页，无论你是要面试，还是提升自己的修为，我想它都一定能帮助你，否则找我要红包！目录如下

免费送给大家，只求来个赞

程序员内功修炼epub版：链接:https://pan.baidu.com/s/1WaCyiuEUv6dctOH6gaLbOg 密码:9svz

程序员内功修炼PDF版：链接:https://pan.baidu.com/s/1TDuD1rr1LTCMlWfSgVon7g 密码:4irm

1、点赞，可以让更多的人看到这篇文章

2、关注我的原创微信公众号『帅地玩编程』，第一时间阅读我的文章，已写了 150+ 的原创文章。

作者：帅地，一位热爱、认真写作的小伙，目前维护原创公众号：『帅地玩编程』，已写了150多篇文章，专注于写 算法、计算机基础知识等提升你内功的文章，期待你的关注。

希望本文不仅能告诉你什么是动态规划，也能给你一种如何分析、求解动态规划问题的思考方式。

1. 运筹学中的动态规划

动态规划(Dynamic Programming，简称DP)是运筹学的一个分支，它是解决多阶段决策过程最优化的一种数学方法。把多阶段问题变换为一系列相互联系的的单阶段问题，然后逐个加以解决。

这里提到动态规划其实是一种数学方法，是求解某类问题的一种方法，而不是一种特殊的算法，没有一个标准的数学表达式或明确定义的一种规则。

比如我们接触过的”排序算法“，”二叉树遍历算法“等，这些算法都是有固定范式的，遇到此类问题我们只需要照搬算法即可。但动态规划却不是，它告诉你的是解决某类问题的一种思路，或者是一种更高意义上的算法，是一种道，而不是术。所以动态规划难就难在我们即使学会了这种思想，遇到具体问题也需要具体分析，很可能因为我们构造不出动态规划所需要的形式而无法解决，甚至根本想不到这是一个动态规划问题。

如下图。我们在解决某些最优问题时，可将解决问题的过程按照一定次序分为若干个互相联系的阶段（1, 2, ..., N），从而将一个大问题化成一系列子问题，然后逐个求解。

在每一个阶段都需要作出决策，从而使整个过程达到最优。各个阶段决策的选取仅依赖当前状态（这里的当前状态指的是当前阶段的输入状态），从而确定输出状态。当各个阶段决策确定后，就组成了一个决策序列，这个决策序列就决定了问题的最终解决方案。这种把一个问题可看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程。

前面说到”仅需要依赖当前状态“，指的是问题的历史状态不影响未来的发展，只能通过当前的状态去影响未来，当前的状态是以往历史的一个总结。这个性质称为无后效性(即马尔科夫性)。 上图中，在阶段2时所做出的决策，仅依赖于阶段2的输入状态，与阶段1的输入状态无关。

动态规划定义中提到按照一定次序分成互相联系的子阶段，这里面的关键是互相联系。如果是独立的子问题，那是分治法，分而治之的意思。动态规划将一个大问题化成一族互相联系、同类型的子问题。既然是同类型，我们在逐个解决子问题的时候，就可以利用相同的决策，从而更容易的解决问题。互相联系利用前面已经解决的子问题的最优化结果来依次进行计算接下来的子问题，当最后一个子问题得到最优解时，就是整个问题的最优解。

这里面包括两个关键点：

1. 每一个阶段可能包括很多状态，前后阶段的状态通过决策联系在一起。如果要利用前阶段子问题的结果解决现阶段的子问题，必须要能够建立前后阶段状态的转移关系，最好可以通过方程表示。用专业术语我们又叫做”状态转移方程“。
2. 我们在衡量最优解的时候需要有一个指标函数，最优解就是让这个指标函数达到最优值，比如最大或者最小。如果我们可以将问题拆分成子问题，那么这个指标函数也必须具有分离性，也就是必须能够利用子问题的最优递推的求出整体最优。当整体最优求解出以后，就可以知道各个子问题的最优解。

可以看到，上面两个关键点无论是状态转移方程还是指标函数分离，其实都是需要列出递推关系式，如果恰当的选取状态，让每个子问题的状态能够表示出子问题的最优解，那我们就可以用状态转移方程递推求出指标函数的最优解。实际中我们也是经常这么做的。

2. 动态规划举例

上面的描述如果觉得有些抽象，可以看完下面的栗子再回过头看一遍，可能理解会更加深刻。如下图，要求出从A点到F点的最短路径。我们来分析一下如何用动态规划的思想来解决这个问题。

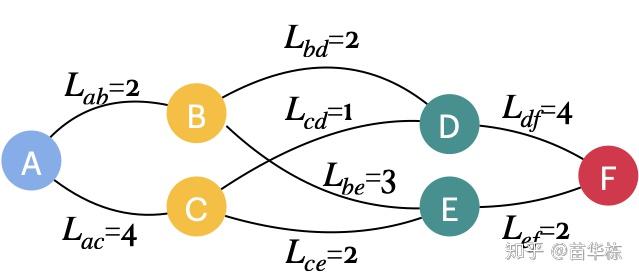
第一步，我们将这个问题拆分成多阶段子问题，然后选择状态变量，使其满足无后效性。如下图，我们分为3个阶段。阶段1有1个输入状态A，输出状态B, C，阶段1的输出状态就是阶段2的输入状态，所以阶段2有2个输入状态{B, C}，阶段3有2个输入状态{D, E}，输出状态F。

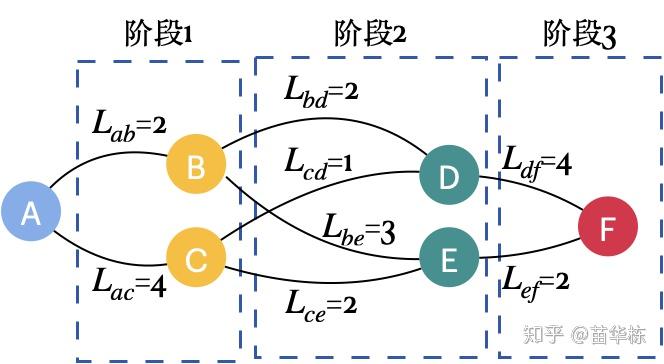
以状态D为例，从状态D做决策选择最短路径的时候，我们只关心如何从D到F，不关心从前一阶段是从B还是C到达的D，满足无后效性。

第二步，确定决策集合。假设当前处在状态B，此时的允许决策集合就是{ D, E}，不同的决策会使得状态转移的路径不同，从而影响到下一个状态。当选择决策D时，对应的决策变量 。

第三步，确定状态转移方程、分离指标函数。

把从A到F的路径看成一个指标函数，这个指标函数的最小值就是最短路径。我们接着分离指标函数，找到递推关系。

我们用 表示从初始节点到第k阶段节点s的最短路径，当我们这样拆成子问题时，它既是整个问题的最优子结构（因为当k为N时，就是原问题本身），又可以定义成状态。 如果我们可以列出状态转移方程，也就可以递推求出最优解。

,

接下来就是如何利用最短路径推导出 ，从而构造出递推方程。我们有

同理有

有了上面这个状态转移方程，我们可以容易的求出

于是，上述问题的最短路径就是7。

3. 《算法导论》中的动态规划

动态规划的思想最初是由美国数学家贝尔曼在1951提出，前面我们也是从数学的角度去理解动态规划，它背后的思想是最优化定理。

在《算法导论》中也讲到了”动态规划“，我在前面提到，动态规划难就难在它不是一成不变的，是一种更高意义上的算法思想；它不是一种特殊的招式，而是无招胜有招，需要见招拆招。

从算法的角度来看，什么时候可以使用动态规范方法解决问题呢？这其中包括了两个要素，分别是”重叠子结构“和”最优子结构“。下面我们就借鉴《算法导论》，从算法的维度再来剖析一遍动态规划，看看和运筹学中的”动态规划“能不能找到什么共性？

1）重叠子结构

前面我们说动态规划是将一个多阶段问题分成几个相互联系的单阶段问题。而这几个相互联系的单阶段问题一定要是一族同类型的子问题，这样分成多阶段决策才是有意义的，否则我们每次面对的决策都是不同的问题，也就失去了分成单阶段的意义。

在算法上，我们把这种同类型的子问题又叫做”重叠子结构“。重叠不是相同，而是同类型，我们必须得利用前面子结构计算出的结果，用递推不断地调用同一个问题。

所以说，《算法导论》中的重叠子结构其实就是对应了数学中将多阶段问题分成单阶段问题的过程，只不过强调了这个单阶段问题必须是”重叠的“，这样才能够用同一种算法递推地解决问题。

2）最优子结构

利用前面已经解决的子问题最优解来构造并解决后面的子问题。能够构造的前提就是要满足指标函数的分离性，也就是全局最优解一定能够拆成子问题的最优解，从而递推解决。

对应到算法中，就是按照自底向上的策略，首先找到子问题的最优解，解决子问题，然后逐步向上找到问题的一个最优解。也就是说，整体问题的最优解包括了子问题的最优解。我们又叫做”最优子结构“。

这么分析来，《算法导论》中的最优子结构其实就是对应了数学中指标函数的分离性。两者只是从不同的维度描述而已。

所以动态规划在数学上和算法上的描述归根到底都是相同的，只是使用数学语言和算法语言的区别。

于是我们按照定义看看如何辨别DP问题。

先来看看必须提到的斐波那契数列，它的递推表达式为

• 从数学上来看，这个问题本身不是一个最优化问题，也就是没有一个指标函数去衡量最优值；而且需要依赖当前状态和前一个状态，不满足无后效性。所以从数学上来说它不是一个动态规划问题。
• 从算法上看，它虽然具有重叠子结构，但本身不是一个最优化问题，没有最优子结构，不是动态规划问题。虽然不满足无后效性，但是依赖有限个状态，同样可以列出状态转移方程。

虽然不是DP问题，但我们也没有必要那么教条，毕竟动态规划是用来一系列比较复杂的最优化问题，当然也可以利用动态规划当中的一些思想去解决类似的问题，因为相对于动态规划问题，斐波那契数列这种问题算是太小儿科了。

接下来我们看看什么样的问题是动态规划问题，以及如何运用上面介绍的步骤进行解题。

学了这么多动态规划的知识，需要刷刷题，由简入难，体会一下动态规划到底怎么用，如何将这种思想付诸于实践。如果觉得学的比较明白了，也需要刷刷题打击一下自信。（下面所有的解法都是为了详细提现如何使用动态规划，所以在时间复杂度和空间复杂度上都没有经过优化）

题目来自LeetCode

53. 最大子序和 (难度：简单)

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
示例: 输入:[-2,1,-3,4,-1,2,1,-5,4], 输出: 6
解释: 连续子数组[4,-1,2,1]的和最大，为 6。

虽然难度为简单，但我觉得从动态规划的角度来考虑，这道题一点也不简单。

首先找关键字，要求最大子序和，有关键字”最大“，是一道最优问题，可能是一道DP问题。

接下来就是最关键的一步，也是最难的一步。如何构造出子问题，每个子问题必须满足”重叠子结构“和”最优子结构“两个要求才能用动态规划来解决。

首先想到的是如果原问题是”N个元素的最大子序和“，那子问题能不能是”N-1个元素的最大子序和“，也就是能否找到N-1个元素最大子序和跟N个元素最大子序和的递推关系，并且能用同类型的算法去解决。如何可以找到，就满足”重叠子结构“和”最优子结构“。

首先来看其中的一种情况。

如果我们求出了 ，其中 表示从第1个元素到第N个元素的最大子序和，如下图。那么的解对的解有没有帮助呢？也就是能不能求出 和 的递推关系呢？

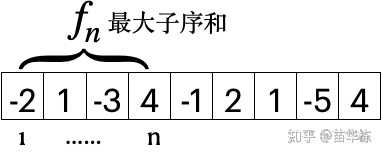
容易得出 ，最大子序列是第2个元素1。而 ，最大子序列是第4个元素4。求最大子序和必须找到最大子序列，当我们求 时，由于 中最大子序列的位置是不知道的，所以新增加一个元素时，这个元素是否能添加到前面的最大子序列中也是不知道的。比如对于子序列{ 2, -2}，最大子序和为2，新添加一个元素后子序列变为{2, -2, 1}，此时虽然添加了一个正的元素1，但无法利用前一个最大子序列，因为无法判断是否应该连在一起构成一组新的最大子序列。

所以这里问题就来了，这种子问题的构造方式无法构成”最优子结构“，也就是子问题的最优解无法递推地解决下一个子问题，无法列出状态转移方程，也就不能用动态规划来解决。所以说即使理解动态规划，但是子问题的构造方式还是十分有技巧的，否则动态规划的大招还是使不出来。我们要换另外一种构造子问题的方式。

前面构造的子问题是”前N个元素的最大子序和“，产生了一个问题，在增加一个新元素的时候，不知道前一个最大子序列的位置，所以无法判断新添加的元素是否应该加到前面的子序列中，因为有可能被中间不在子序列中的元素打断，所以也就无法构造最优解。

那如果想要新添加的元素不被中间的元素打断，就得在构造子序列 的时候保证每一个子序列都是以第n个元素结尾。于是子问题变为"前N个元素中以第N个元素结尾的最大子序和"。

如上图，第n个元素为-3，子序列中必须包含这个元素，所以

这样，新添加一个元素4构成 的时候，我们只需要判断 是否为正即可。如果是正数，对子序列和起到正增益的作用，则包含到新的子序列中；否则，抛弃前面的子序列。例如

于是，我们可以构造出 的递推关系

胜利就在前方，但是这样构造有一个问题，要求的是最大子序和，而不是以某个元素结尾的最大子序和。但是无论是最大子序列是什么，一定是以1 - N当中的某一个元素结尾，所以前面拆分的子问题是最优子问题，我们只需要找到最优子问题当中解的最大值，就是最终问题的解。下面上代码

public class MaxSubArray {
    public static int maxSubArray(int[] nums) {
        // 构造子问题，dp[n]代表以n结尾的最大子序和
        int[] dp = new int[nums.length];
        // 状态初始化
        dp[0] = nums[0];
        int ans = nums[0];
        for (int i = 1; i < dp.length; i++) {
            // 分离指标函数，列出状态转移方程
            dp[i] = Math.max(dp[i - 1], 0) + nums[i];

            // 最优解是最优子结构当中的最大值
            ans = Math.max( ans, dp[i] );
        }
        return ans;
    }

    public static void main(String[] args) {
        int[] nums = new int[]{-2, 1, -3, 4, -1, 2, 1, -5, 4};
        System.out.println("MaxSubArray Length=" + maxSubArray(nums));
    }
}

输出结果

MaxSubArray Length=6

通过这个问题可以看到，动态规划最难的部分是构造状态，使其满足最优子结构，并且列出状态转移方程。如果这部分完成了，那代码其实就是将我们的思路写下来而已。

72. 编辑距离 (难度：困难)

据说这道题也是鹅厂的面试题，在测量两段基因相似度的时候会采用编辑距离这一概念，编辑距离越短，则基因越相似。

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作：
1. 插入一个字符
2.删除一个字符
3.替换一个字符
示例: 输入: word1="horse", word2="ros" 输出:3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

同样，看到了关键字”最少“，应该是一道DP问题。

首先，构造子问题1 word1="h"，word2=”r"时的最小操作数 ,其中下标1,1表示word1和word2的字符串长度都是1。但是即使知道这个最少操作数，如何构造下一个子问题呢？下个子问题貌似还不明确，也就是没有找到状态转移方程，那么其实状态还是没有被明确定义出来。下一个子问题应该如何定义字符串呢？我试着将问题最简化，子问题2只在word1增加一个字符，变为 word1="ho"，word2="r"的最少操作数 。显然，子问题2的最少操作数就是在子问题1基础上将字符'o'删除，也就是 。那如果有一个子问题2’是word1="h"，word2="ro"，同样，就是在子问题1基础上增加一个字符'o'，也就是 。我可能会想到列出这样一个等式

但很快，我就会发现这个等式有一个问题，如果要求 ，是应该用 还是用 呢？由于要最少操作数，我可能会把上面的式子改成

好像已经找到状态转移方程了。不会这么简单吧，我们回头看一看题目，状态转移方程中仅用到了插入，删除两个操作，还少了一个替换字符的操作，也就是如果已经得出来 ，我只需要将两个字符串中位于m+1和n+1的字符串进行替换，同样也可以实现转换。于是我再修正一下上式，使其包含替换的操作

细心的朋友可能会想到，替换的操作不一定是必须的。比如题目中给的例子，如果解决了word1=”h"，word2=”r“这个子问题1解决了以后，那么对于word1="ho", word2="ro"这个子问题也就解决了，因为最后一个字符是相同的，无需任何操作。所以上面的方程还需要改造。

状态转移方程我们已经列出来了，我们用表格来展现一下上面的关系。

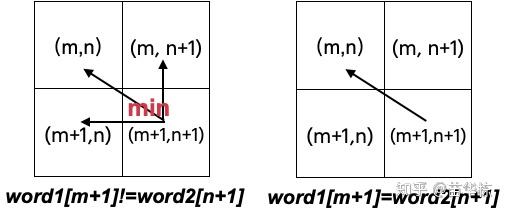
但是递归需要初始条件，那怎么进行初始化呢？从上面的表格来看，也就是如何初始化表格的最左侧一列和最上面一行。

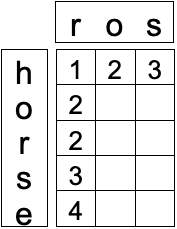
到此，有了初始化条件和状态转移方程，我们就可以写具体实现了。这样初始化虽然可以实现，但有一个不太好的地方，就是初始化是需要依赖输入字符串，如果出现相同字符，初始化值是不同的。而我们希望的是一套统一的算法，无论输入字符串是什么，初始化方式是固定的。那么我们应该如何改造初始化，让它不依赖于输入字符串呢？那就是初始子问题尽量的简单。上面的初始化对应的是 和 ，我们能不能再简化初始化条件？让 和 由更基本的初始化条件推导出来呢？所以我们需要定义 和 ，那 对应的就是空字符，如下图。

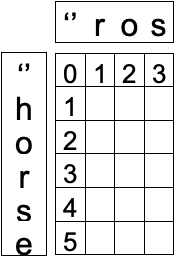
有了空字符，则初始化条件就简单了，由空字符生成任意字符串，都是加字符，所以第一行和第一列对应的就是字符个数，这样初始化条件就简单了。而其它的位置，我们只需要按照前面的递推关系填进去就可以了，如下图，有点像填杨辉三角形。

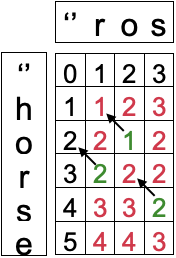
其中绿色的部分是因为字符相同，直接取左上方的值，其它则是取左，上，左上方的最小值加1。表格填完了，下面按照前面的思路上代码，

public class MinDistance {
    public static int minDistance(String a, String b) {
        int length1 = a.length();
        int length2 = b.length();
        int[][] dp = new int[length1 + 1][length2 + 1];
        
        // 初始化第一列
        for (int row = 0; row < length1 + 1; row++) {
            dp[row][0] = row;
        }
        // 初始化第一行
        for (int column = 0; column < length2 + 1; column++) {
            dp[0][column] = column;
        }

        for (int row = 1; row < length1 + 1; row++) {
            for (int column = 1; column < length2 + 1; column++) {
                // 如果字符相等，则直接取左上方的值
                if ( a.charAt(row - 1) == b.charAt(column - 1) ) {
                    dp[row][column] = dp[row-1][column-1];
                } else { // 否则取左，上，左上三个值中的最小值+1
                    dp[row][column] = Math.min(
                        dp[row-1][column-1], 
                        Math.min(
                            dp[row][column-1], 
                            dp[row-1][column] 
                        )) + 1;
                }
            }
        }
        // 递推后，表格最右下方的值就是整个问题的最优解
        return dp[length1][length2];
    }

    public static void main(String[] args) {
        String a = "horse";
        String b = "ros";
        System.out.println("minDistance Result: " + minDistance(a, b));
    }

}

输出结果

minDistance Result: 3

887. 鸡蛋掉落 （难度：困难）

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。 每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。 你知道存在楼层 F ，满足 0 <=F <=N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。 每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <=X <=N）。 你的目标是确切地知道 F 的值是多少。 无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？ 示例 1： 输入：K=1, N=2 输出：2
解释： 鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F=0 。 否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F=1 。 如果它没碎，那么我们肯定知道 F=2 。 因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

这道题也很经典，作为思考题吧。

解释了两道题，相信已经对动态规划有一定感觉了，难点不是动态规划本身，而是如何准确的定义状态，列出状态转移方程。从我的经验来看，可以按以下两个方法尝试

1. 将问题简化成最简，定义状态，这样更有利于观察到问题本质，寻找递推关系。
2. ”大胆假设，小心求证“。在定义状态的时候，如果无法找到状态转移方程，可以大胆尝试几种不同的状态定义方式，不要怕错，然后再仔细考察是否满足最优子结构，列出状态转移方程。